Algoritmul lui Prim

În acest tutorial, veți afla cum funcționează algoritmul lui Prim. De asemenea, veți găsi exemple de lucru ale algoritmului Prim în C, C ++, Java și Python.

Algoritmul lui Prim este un algoritm minim de copac care ia un grafic ca intrare și găsește subsetul marginilor acelui grafic care

formează un copac care include fiecare vârf
are suma minimă a greutăților dintre toți arborii care pot fi formați din grafic

Cum funcționează algoritmul lui Prim

Se încadrează într-o clasă de algoritmi numiți algoritmi lacomi care găsesc optimul local în speranța de a găsi un optim global.

Începem de la un vârf și continuăm să adăugăm margini cu cea mai mică greutate până când ne atingem obiectivul.

Pașii pentru implementarea algoritmului Prim sunt după cum urmează:

Inițializați arborele minim cu un vârf ales la întâmplare.
Găsiți toate marginile care conectează copacul la vârfuri noi, găsiți minimul și adăugați-l la copac
Repetați pasul 2 până când obțineți un copac minim

Exemplu de algoritm al lui Prim

Începeți cu un grafic ponderat

Alegeți un vârf

Alegeți cea mai scurtă margine din acest vârf și adăugați-o

Alegeți cel mai apropiat vârf care nu este încă în soluție

Alegeți cea mai apropiată margine care nu este încă în soluție, dacă există mai multe opțiuni, alegeți una la întâmplare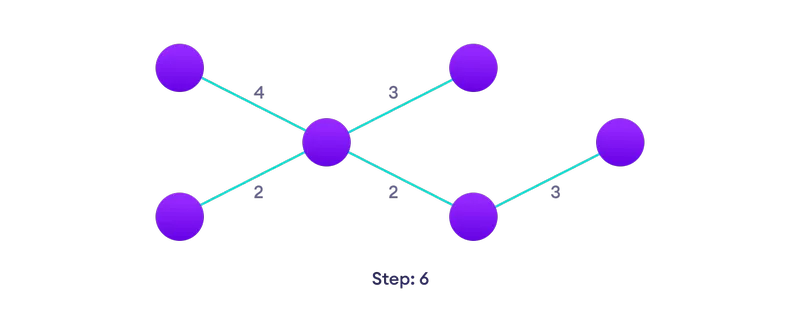

Repetați până când au un copac întins

Pseudocodul algoritmului lui Prim

Pseudocodul pentru algoritmul prim arată cum creăm două seturi de vârfuri U și VU. U conține lista vârfurilor care au fost vizitate și VU lista vârfurilor care nu au fost vizitate. Unul câte unul, mutăm vârfurile de la setul VU la setul U conectând marginea cu greutatea cea mai mică.

 T = ∅; U = ( 1 ); while (U ≠ V) let (u, v) be the lowest cost edge such that u ∈ U and v ∈ V - U; T = T ∪ ((u, v)) U = U ∪ (v)

Exemple Python, Java și C / C ++

Deși este utilizată reprezentarea matricii de adiacență a graficelor, acest algoritm poate fi implementat și folosind Adjacency List pentru a-și îmbunătăți eficiența.

Python Java C C ++

 # Prim's Algorithm in Python INF = 9999999 # number of vertices in graph V = 5 # create a 2d array of size 5x5 # for adjacency matrix to represent graph G = ((0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)) # create a array to track selected vertex # selected will become true otherwise false selected = (0, 0, 0, 0, 0) # set number of edge to 0 no_edge = 0 # the number of egde in minimum spanning tree will be # always less than(V - 1), where V is number of vertices in # graph # choose 0th vertex and make it true selected(0) = True # print for edge and weight print("Edge : Weight") while (no_edge  G(i)(j): minimum = G(i)(j) x = i y = j print(str(x) + "-" + str(y) + ":" + str(G(x)(y))) selected(y) = True no_edge += 1

 // Prim's Algorithm in Java import java.util.Arrays; class PGraph ( public void Prim(int G()(), int V) ( int INF = 9999999; int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false boolean() selected = new boolean(V); // set selected false initially Arrays.fill(selected, false); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in // graph // choose 0th vertex and make it true selected(0) = true; // print for edge and weight System.out.println("Edge : Weight"); while (no_edge < V - 1) ( // For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise // choose another vertex nearest to selected vertex at step 1. int min = INF; int x = 0; // row number int y = 0; // col number for (int i = 0; i < V; i++) ( if (selected(i) == true) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) System.out.println(x + " - " + y + " : " + G(x)(y)); selected(y) = true; no_edge++; ) ) public static void main(String() args) ( PGraph g = new PGraph(); // number of vertices in grapj int V = 5; // create a 2d array of size 5x5 // for adjacency matrix to represent graph int()() G = ( ( 0, 9, 75, 0, 0 ), ( 9, 0, 95, 19, 42 ), ( 75, 95, 0, 51, 66 ), ( 0, 19, 51, 0, 31 ), ( 0, 42, 66, 31, 0 ) ); g.Prim(G, V); ) )

 // Prim's Algorithm in C #include #include #define INF 9999999 // number of vertices in graph #define V 5 // create a 2d array of size 5x5 //for adjacency matrix to represent graph int G(V)(V) = ( (0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)); int main() ( int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false int selected(V); // set selected false initially memset(selected, false, sizeof(selected)); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in //graph // choose 0th vertex and make it true selected(0) = true; int x; // row number int y; // col number // print for edge and weight printf("Edge : Weight"); while (no_edge < V - 1) ( //For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise //choose another vertex nearest to selected vertex at step 1. int min = INF; x = 0; y = 0; for (int i = 0; i < V; i++) ( if (selected(i)) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) printf("%d - %d : %d", x, y, G(x)(y)); selected(y) = true; no_edge++; ) return 0; )

 // Prim's Algorithm in C++ #include #include using namespace std; #define INF 9999999 // number of vertices in grapj #define V 5 // create a 2d array of size 5x5 //for adjacency matrix to represent graph int G(V)(V) = ( (0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)); int main() ( int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false int selected(V); // set selected false initially memset(selected, false, sizeof(selected)); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in //graph // choose 0th vertex and make it true selected(0) = true; int x; // row number int y; // col number // print for edge and weight cout << "Edge" << " : " << "Weight"; cout << endl; while (no_edge < V - 1) ( //For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise //choose another vertex nearest to selected vertex at step 1. int min = INF; x = 0; y = 0; for (int i = 0; i < V; i++) ( if (selected(i)) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) cout << x << " - " << y << " : " << G(x)(y); cout << endl; selected(y) = true; no_edge++; ) return 0; )

Prim's vs Algoritmul lui Kruskal

Algoritmul lui Kruskal este un alt algoritm popular de copac minim care folosește o logică diferită pentru a găsi MST-ul unui grafic. În loc să pornească de la un vârf, algoritmul lui Kruskal sortează toate marginile de la greutate redusă la mare și continuă să adauge cele mai joase margini, ignorând acele margini care creează un ciclu.